Ez egy AI által fordított bejegyzés.
Logikai adatmodellezés
- Írás nyelve: Koreai
- •
-
Referencia ország: Minden ország
- •
- Informatika
0000-00-00 00:00:00
Válasszon nyelvet
A durumis AI által összefoglalt szöveg
- A logikai adatmodellezés a konceptuális adatmodellezésnek a relációs adatbázis-paradigmához igazodó átalakítása, amely a leképezési szabályokon alapul.
- A relációs adatbázisokban az 1:1, 1:N, N:M relációk kezelésének módját, a közbenső táblák létrehozásának módját, valamint a normalizálás fontosságát és a három szakaszt (1NF, 2NF, 3NF) részletesen bemutatja.
- Világosan bemutatja az egyes normalizálási lépések célját és elveit, különösen a 3. normalizálási lépés során a tranzitív függőségek eltávolításának folyamatát részletesen leírja.
A követelmények elemzése és a konceptuális adatmodellezéshez képest a logikai adatmodellezés egy sokkal mechanikusabb eljárás.
A lényeg a konceptuális adatmodellezés kimeneti ERD-jét a relációs adatbázis paradigma szerint átalakítani a hozzárendelési szabályok (Mapping Rule) alapján.
Hozzárendelési szabályok
- A négyzet alakú entitásokat táblákká alakítják át.
- A kerek attribútumokat oszlopokká alakítják át.
- A kapcsolatokat PK-kká vagy FK-kká alakítják át.
Először is a FK nélküli táblákat könnyebb megjeleníteni.
Kapcsolatok
- A táblák közötti kapcsolatot a kardinalitás és az opcionális jelleg figyelembevételével jelenítik meg.
- A legegyszerűbb kapcsolat, az 1:1 kapcsolat, majd az 1:N kapcsolat, végül az N:M kapcsolat jelenik meg.
Az 1:1 kapcsolat kezelése
Az 1:1 kapcsolatban a két tábla közötti függőségi viszonyt vizsgálják, és beállítják az FK-t.
Szülő és gyermek táblaként tekinthetünk rájuk.
Az 1:N kapcsolat kezelése
Az 1:N kapcsolatban az 1-et az N hivatkozza, ezért az N-ben van az FK.
Az N:M kapcsolat kezelése
A relációs adatbázisban az N:M kapcsolat kezeléséhez egy közbenső táblát (ún. leképezési vagy összekapcsoló táblát) kell létrehozni.
Fontos, hogy a leképezési tábla esetében meg kell adni a hozzárendelt táblák kardinalitását és opcionális jellegét.
Normalizálás (Normalization)
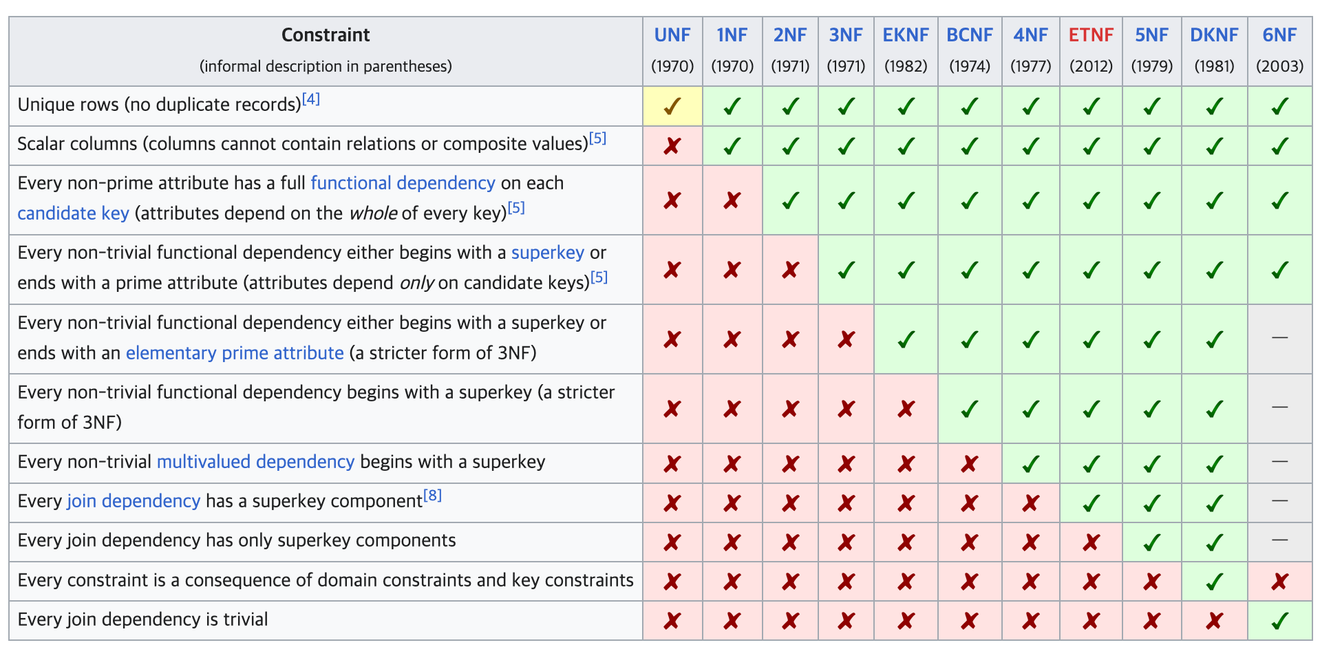
Wikipedia - Adatbázis normalizálás
Az a folyamat, amelynek során a nem finomított táblákat relációs adatbázishoz illő táblákká alakítják át.
Az iparban használt normalizációs folyamat a 3. normalizációs szintig terjed, az azt követő normalizációs szinteket elsősorban tudományos célokra használják.
A normalizálást lépésről lépésre kell végrehajtani, egyszerre egy szintet.
1. normalizációs szint (1st Normal Form, 1NF)
- Az oszlopnak atomikus értékeket kell tartalmaznia.
A 1. normalizációs szint fő elvének megértése nehéz lehet, de egyszerűen azt jelenti, hogy minden oszlopnak egyetlen értéket kell tartalmaznia.
Ha egy oszlopban több érték van, vagyis nem atomikus, akkor az SQL-parancsokkal való összekapcsolás is nehézkes lehet, és különböző problémákat okozhat.
2. normalizációs szint (2nd Normal Form, 2NF)
- Meg kell felelni az 1. normalizációs szintnek.
- El kell távolítani a részleges függőségeket.
Ha egy tábla sorában ismétlődő értékek vannak, akkor meg kell keresni az adott sortól függő oszlopokat, és el kell őket választani.
3. normalizációs szint (3rd Normal Form, 3NF)
- Meg kell felelni az 1. normalizációs szintnek.
- Meg kell felelni a 2. normalizációs szintnek.
- El kell távolítani a tranzitív függőségeket.
A tranzitív függőség kifejezés nagyon nehéz megérteni. Úgy tűnik, hogy ha egy adott táblában van egy vagy több olyan érték, amely implicit módon egy másik tábla azonosítóját jelenti (természetesen az FK-t leszámítva), akkor az tranzitív függőségnek nevezik.
